|
130 лет со дня рождения Бориса Сергеевича
Ястремского
 |
|
Борис Сергеевич Ястремский (1877-1962)
|
9 мая 2007 года исполнилось 130 лет со дня рождения
Бориса Сергеевича Ястремского, статистика, математика, профессора
(1924), доктора экономических наук (1932), заслуженного деятеля
науки РСФСР (1942), автора научных работ теоретического и прикладного
характера в области математической статистики, теории статистики,
сельскохозяйственной статистики и демографии1.
Борис Сергеевич Ястремский родился 9 мая 1877 года в
Харьковской губернии (Дергачи) в семье известного революционера
народовольца С. В. Ястремского и воспитывался в традициях русских
революционеров прошлого века. В 1896-1900 годах учился на физико-математическом
факультете Харьковского университета и в Женевском университете.
Участвовал в революционном движении, подвергался арестам и ссылкам.
В 1900 году началась практическая статистическая деятельность Ястремского.
С 1909 года Ястремский - секретарь математико-статистической секции
Общества страховых знаний, позднее генеральный секретарь этого общества.
После октября 1917 года Б.С. Ястремский был привлечен
к работе по созданию советской государственной статистики, он заведовал
отделом статистики Комиссариата по делам страхования, продолжительное
время работал в отделе методологии ЦСУ СССР, занимаясь вопросами
страховой и сельскохозяйственной статистики. В 1918-1926 годах он
был членом коллегии ЦСУ, в 1931 году - членом Госплана СССР. Одновременно
преподавал математическую статистику, затем теорию статистики на
Центральных статистических курсах ЦСУ (1919), в МГУ (1921), в МИНХе
(1925-1930), во Всесоюзной плановой академии (1931-1940), в Московском
институте народнохозяйственного учета (1932). С 1933 года и до последних
дней жизни основным местом работы Б.С. Ястремского был МЭСИ, где
он в разное время возглавлял кафедру математической статистики.
Более чем полувековая творческая жизнь Б. С. Ястремского
охватывает многие проблемы статистической науки и практики, которым
посвящено 97 его опубликованных работ.
Среди учеников Б. С. Ястремского - известные советские
статистики А.Я. Боярский, Л.С. Бранд, А. М. Вахатов, И. Г. Венецкий,
А. И. Ежов, Я. И. Лукомский, И. С, Малышев, В. И. Манякин, И. Ю.
Писарев, Т. В.Рябушкин, С. В. Сазонов, В. Н. Старовский, Б. Ц. Урланис,
П. П. Шушерин и многие другие.
Б.С. Ястремский скончался в 1962 году, оставив о себе
память как об одном из замечательных людей нашего времени, посвятившем
свою жизнь служению статистике. Его труды - свидетельство неутомимости
в поисках нового, заботы о развитии теории и практики статистики,
диалектичности его мышления. Он был яростным в идейной борьбе, но
добрым другом для товарищей по работе, для своих учеников и коллег,
для всех окружающих.
Ниже публикуется краткий отрывок из воспоминаний Б.Ц.
Урланиса, слушавшего лекции Бориса Сергеевича в Московском университете,
а также небольшая статья Б.С. Ястремского "Связь между показателями
воспроизводства населения", опубликованная впервые в 1945 году
в качестве приложения к "Курсу демографической статистики"
А.Я. Боярского.
Из воспоминаний Б.Ц. Урланиса2:
Курс "Элементы высшей математики" читал Б.С.
Ястремский… Свой курс Б.С. Ястремский читал вполне квалифицированно,
но совершенно не учитывал уровень математических знаний студентов.
Я лично очень плохо усваивал преподносимый им материал. Он прямо,
можно сказать, огорошил студентов бесконечным количеством различных
функций, давая на лекциях громоздкие формулы, которые потом мне
ни разу не оказались нужными во всей моей последующей деятельности.
Он, например, много внимания уделял тригонометрическим функциям,
трансцендентным функциям, строке Тейлора и ее частному случаю -
строке Маклорена - все это было для нас очень трудноусвояемым материалом.
Надо учесть, что и в элементарной математике студенты тогда были
очень слабо подготовлены: многие из них кончили рабфаки, где преподавание
математики было очень сокращенным, а те, кто кончил среднюю школу,
как я, во время занятий больше были в то время озабочены тем, как
избавиться от чувства голода, чем тем, чтобы разобраться в алгебре.
Мне, кстати сказать, особенно не повезло в этом отношении, так как
в школе, где я учился, был очень симпатичный, добрый преподаватель
математики, у которого можно было почти совсем не учиться! Конечно,
такая доброта кроме вреда для учащегося ничего не может дать. Это
дало мне повод уже много позднее написать в стенгазете МГУ статью
под названием "Строгий педагог - друг студента". Либерализм
преподавателя несет в себе большую опасность, это надо помнить всем
молодым педагогам.
Трудность изложения материала, подававшегося Б.С. Ястремским,
привела к тому, что в студенческие годы я не понял основных идей
дифференциального и интегрального исчисления, красота которых открылась
для меня уже после окончания Университета.
Вообще же надо сказать, что Б.С.Ястремский сыграл большую
роль в развитии советской математической статистики. Он предложил
способ сглаживания динамических рядов скользящими отрезками парабол.
Этот способ в математической науке носит его имя. Позже я с ним
познакомился ближе, он многие годы был моим соседом за столом президиума
Статистической секции Московского Дома ученых. Я как-то был у него
на квартире и заснял на киноленту, как он вертит ручку арифмометра,
как он угощает гостей за столом и еще какие-то сценки. Он был большим
"поклонником" закона нормального распределения, применяя
и трактуя его с позиций диалектического материализма. Умер он в
возрасте 85 лет.
Связь между показателями воспроизводства населения3
Б.С. Ястремский
§ 1. Используемые демографической статистикой
показатели воспроизводства населения - рождаемость, фертильность
(плодовитость), коэффициенты воспроизводства населения брутто и
нетто, детность - связаны между собой корреляционной зависимостью.
В основе этой корреляционной зависимости, как показало произведенное
нами в 1941-1945 гг. исследование, лежит функциональная связь между
плодовитостью женщин и их возрастом. Нами найдено аналитическое
выражение такой функциональной связи (см. § 2). Получилось оно в
результате поисков обобщения многочисленных статистических данных,
как советских, так и зарубежных, преимущественно за период 1930
- 1940 гг. Всюду найденное мною выражение безотказно отображало
характерные черты зависимости плодовитости женщин от их возраста4.
§ 2. Аналитическое выражение упомянутой выше
функциональной зависимости представляет плодовитость Fx как
функцию возраста x, характеризуемую следующими четырьмя параметрами:
- начальный возраст c, с которого начинается
период деторождения женщин; этот возраст в разных странах колеблется
в пределах 16±2 года;
- оптимальный возраст а, при котором плодовитость
достигает максимальной величины Fa; этот возраст в разных
странах колеблется в пределах 27±4 года;
- конечный возраст b, на котором заканчивается
период деторождения женщин; данный возраст колеблется в разных
странах в пределах 53±6 лет;
- четвертый параметр k характеризует общую
высоту плодовитости; этот параметр может быть замещен пропорциональной
ему величиной плодовитости Fa оптимального возраста a;
этот параметр Fa в разных странах колеблется в весьма широких
границах -от 100 до 300‰, в отдельных случаях выходя за пределы
этого интервала.
Аналитическое выражение функции Fx имеет следующий
вид:
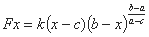
или при замене параметра k другим параметром Fa
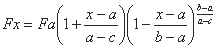
Эта формула для плодовитости еще лучше отвечает фактам,
чем формула Гомперца - Макегама5 для
смертности.
§ 3. Как именно связывается с функцией Fx брутто-коэффициент
воспроизводства Rb?
Коэффициент Rb получает следующее математическое оформление:
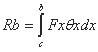
Здесь 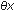 -
доля девочек среди новорожденных детей; эта доля, как известно,
обнаруживает поразительное постоянство, лишь незначительно колеблясь
около величины 0,485±0,005. -
доля девочек среди новорожденных детей; эта доля, как известно,
обнаруживает поразительное постоянство, лишь незначительно колеблясь
около величины 0,485±0,005.
Приняв в расчет указанное выше аналитическое выражение
функции Fx, обнаруживаем после ряда математических выкладок,
что величина Rb может быть представлена в виде произведения
следующих четырех сомножителей:
- величины
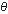 ,
размер которой указан выше; ,
размер которой указан выше;
- параметра Fa;
- разности между средним х и начальным возрастом с
матери; разность эта в разных странах колеблется в сравнительно
узких границах - 12,5± 1,7;
- множителя, имеющего по внешности чрезвычайно сложный
вид, но обнаруживающего поразительное постоянство:
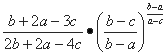
Этот множитель после подстановки:

приобретает следующий вид:
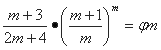
Размеры 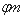 при разных
m изменяются очень слабо, как это видно из следующей таблицы: при разных
m изменяются очень слабо, как это видно из следующей таблицы:
|
m
|
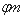
|
m
|
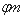
|
|
1,5
|
1,383
|
4,0
|
1,424
|
|
2,0
|
1,406
|
4,5
|
1,423
|
|
2,5
|
1,417
|
5,0
|
1,422
|
|
3,0
|
1,422
|
….
|
….
|
|
3,5
|
1,424
|
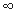
|
1,359
|
Таким образом этот множитель 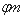 может быть принят равным 1,42.
может быть принят равным 1,42.
Из всех перечисленных четырех сомножителей наибольшей
колеблемостью обладает параметр Fa. Остальные сомножители
могут быть сведены в один почти постоянный множитель, колеблющийся
в разных странах в границах 8,6±0,9.
В результате получается следующее простое выражение,
связывающее коэффициент Rb с параметром Fa:
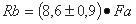
Таким образом величина брутто-коэффициента воспроизводства
почти нацело определяется размерами плодовитости оптимального возраста.
Для общего представления о возможных значениях Rb
в зависимости от тех или иных значений Fa служит следующая
табличка:
Таблица возможных значений Rb при различных величинах
плодовитости оптимального возраста Fa
|
Fa
|
Rb
|
|
100
|
0,86±0,09
|
|
150
|
1,29±0,14
|
|
200
|
1,72±0,18
|
|
250
|
2,15±0,23
|
|
300
|
2,58±0,27
|
§ 4. Нетто-коэффициент воспроизводства Rn
приобретает следующее аналитическое выражение:
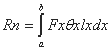
Здесь подынтегральная функция содержит дополнительный множитель
lx, выражающий собой вероятность новорожденной девочке дожить
до возраста х.
Связь между коэффициентами Rb и Rn получает очень
простое выражение, гарантирующее точность до трех значащих цифр:
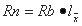
где 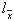 --представляет собой вероятность новорожденной девочке дожить до
среднего материнского возраста
--представляет собой вероятность новорожденной девочке дожить до
среднего материнского возраста 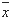 . .
Указанное выше выражение получается в результате учета
того обстоятельства, что изменение функции Fx в пределах
интервала между начальным возрастом с и конечным возрастом
b мало отличается от линейного.
Заметное отклонение от линейности обнаруживается лишь
в конце названного интервала, т. е. как раз там, где величины Fx
оказываются малыми.
Величина х в разных странах колеблется в сравнительно
узких границах: 29±2 года. Что же касается до вероятности 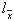 ,
то эта величина варьирует в разных странах довольно сильно. В странах
с высокой рождаемостью ,
то эта величина варьирует в разных странах довольно сильно. В странах
с высокой рождаемостью 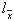 оказывается сравнительно низкой: 0,6-0,7; наоборот, в странах с
низкой рождаемостью она достигает сравнительно больших размеров,
достигая - и даже превышая- величины 0,9.
оказывается сравнительно низкой: 0,6-0,7; наоборот, в странах с
низкой рождаемостью она достигает сравнительно больших размеров,
достигая - и даже превышая- величины 0,9.
Статистический анализ обнаруживает при этом линейную
связь между 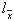 и рождаемостью,
а тем самым и с плодовитостью. и рождаемостью,
а тем самым и с плодовитостью.
С другой стороны, коэффициент Rb, как это показано
было в § 3, связан с плодовитостью также линейно. Следовательно,
коэффициент Rn, представляя собой произведение двух линейных
функций от плодовитости, оказывается связанным с плодовитостью связью
параболической.
Для определения средних размеров Rn по величине
плодовитости Fa нами получена следующая интерполяционная
формула:
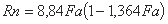
Для суждения о том, как именно связывается коэффициент
воспроизводства Rn с плодовитостью Fa, служит нижеследующая
табличка:
Таблица возможных значений Rn при различных величинах
плодовитости оптимального возраста Fa
|
Fa(‰)
|
Rn
|
|
100
|
0,76±0,11
|
|
150
|
1,05±0,15
|
|
200
|
1,29±0,18
|
|
250
|
1,46±0,20
|
|
300
|
1,57±0,22
|
Установленная выше зависимость коэффициента Rn
от плодовитости основана на обобщении статистических данных зарубежных
стран. Для этих стран характерна обратная зависимость между плодовитостью
и вероятностью дожить до возраста x-.
При использовании этого общего вывода в применении к
оценке советских данных необходимо учитывать следующее обстоятельство.
В условиях социалистического общества, основным и непреложным
принципом которого является забота о человеке, и в первую очередь
забота о детях, не может существовать неразрывной связи между плодовитостью
и доживаемостью, зависящей прежде всего от детской смертности. Социалистическое
общество обладает надлежащими средствами добиться одновременно и
высокой рождаемости и низкой детской смертности.
§ 5. Какова взаимосвязь между рождаемостью и
плодовитостью?
Взаимосвязь эта в первую очередь определяется долей
женщин материнского возраста в общей массе населения. Доля эта при
высокой рождаемости должна быть относительно меньшей по сравнению
с той долей, которая образуется при наличии низкой рождаемости.
Однако, с другой стороны, высокая рождаемость обусловливает расширение
интервала плодовитых возрастов. В результате получается выравнивание
доли женщин материнского возраста в странах с различной рождаемостью.
Статистический анализ подтверждает наличие такого выравнивания.
Поэтому между рождаемостью и плодовитостью, а тем самым и коэффициентом
воспроизводства Rb устанавливается прямая пропорциональная связь.
На основе разработки статистического материала различных
стран нами получено следующее соотношение:

где n - коэффициент рождаемости; Fa -
плодовитость оптимального возраста.
Нижеследующая табличка наглядно иллюстрирует найденную
взаимосвязь
Таблица, характеризующая взаимосвязь между рождаемостью
и плодовитостью Fa
|
Fa‰
|
n‰
|
|
100
|
15±2
|
|
150
|
22±2
|
|
200
|
29±3
|
|
250
|
36±4
|
|
300
|
44±5
|
§ 6. Найденное нами аналитическое выражение зависимости
плодовитости женщин от их возраста (см. § 2) открывает возможность
установления связи между рождаемостью и детностью, т. е. распределением
женщин по числу рожденных ими детей. Разработка этой проблемы пока
еще не закончена.
Таким образом, изложенное исследование увенчалось установлением
связи между следующими показателями воспроизводства населения:
- плодовитостью, характеризуемой плодовитостью оптимального
возраста, т. е. примерно плодовитостью женщин возрастной группы
25-29 лет;
- брутто-коэффициентом воспроизводства;
- нетто-коэффициентом воспроизводства;
- рождаемостью.
Взаимосвязь между перечисленными показателями в их среднем
выражении изображена в нижеследующей результирующей таблице:
|
Оптимальная плодовитость
|
Коэффициент воспроизводства
|
Рождаемость ‰
|
|
Брутто
|
нетто
|
|
100
|
0,86
|
0,76
|
15
|
|
150
|
1,29
|
1,05
|
22
|
|
200
|
1,72
|
1,29
|
29
|
|
250
|
2,15
|
1,46
|
36
|
|
300
|
2,58
|
1,57
|
44
|
Из этой таблицы ясно видна та грань, которая отделяет
расширенное воспроизводство населения от его недопроизводства, т.
е. отвечает простому воспроизводству. Эта грань характеризуется
следующими средними показателями:
- плодовитостью оптимального возраста 140‰,
- брутто-коэффициентом воспроизводства 1,22,
- нетто-коэффициентом воспроизводства 1,00,
- рождаемостью 21‰.
1 - Более подробно о научном вкладе
Б.С. Ястремского можно прочесть в статье А. Боярского и Г. Кильдишева:
Б.С. Ястремский (к 90-летию со дня рождения) //Вестник статистики.
1967. № 5. С. 35-40; См. также Корнев В.П. Видные деятели отечественной
статистики. М.: Финансы и статистики. 1993. С. 101-102.
2 - Б.Ц. Урланис. Неопубликованные воспоминания
//Демоскоп-Weekly. № 253-254, 21 августа-3 сентября 2006 г.( http://www.demoscope.ru/weekly/2006/0253/nauka02.php).
3 - Впервые опубликовано в кн.: Боярский А. Я Курс
демографической статистики. М., 1945. С. 245-249
4 - Найденные зависимости были установлены на эмпирическом
материале о рождаемости и справедливы лишь для возрастных кривых
рождаемости того времени (1930-1940-х годов). Тем не менее работа
сохраняет свое значение как пример оригинального математического
анализа демографических данных.- Ред
5 - Ныне принято написание Мейкем. - Ред.
|